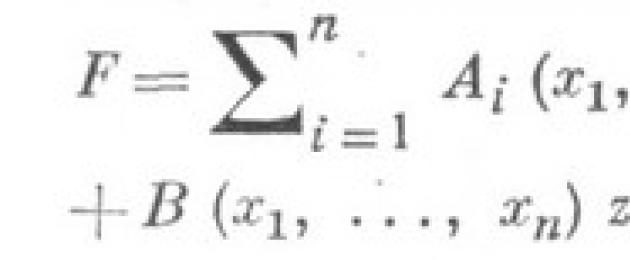(обыкновенное или с частными производными), в к-рое по крайней мере одна из производных неизвестной функции (включая и производную нулевого порядка - саму неизвестную функцию) входит нелинейно. Этот термин обычно употребляют, когда хотят специально подчеркнуть, что рассматриваемое дифференциальное уравнение Н=0 не является линейным, т. е. его левая часть Нне представляет собой линейную форму от производных неизвестной функции с коэффициентами, зависящими только от независимых переменных.
Иногда под Н. д. у. понимается наиболее общее уравнение определенного вида. Напр., нелинейным обыкновенным дифференциальным уравнением 1-го порядка наз. уравнение с произвольной функцией ; при этом линейное обыкновенное дифференциальное уравнение 1-го порядка соответствует частному случаю
Н. д. у. с частными производными 1-го порядка для неизвестной функции z от. пнезависимых переменных имеет вид
где F- произвольная своих аргументов; в случае
такое уравнение наз. квазилинейным, а в случае

Линейным.
Н. Розов.
Математическая энциклопедия. - М.: Советская энциклопедия . И. М. Виноградов . 1977-1985 .
Смотреть что такое "НЕЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ" в других словарях:
Уравнение вида где F заданная действительная функция точки х=(xt, ..., х п)области Dевклидова пространства Е п, и действительных переменных (и(х) неизвестная функция) с неотрицательными целочисленными индексами i1 ,..., in, k=0, ..., т, по… … Математическая энциклопедия
Уравнение, к рое содержит хотя бы одну производную 2 го порядка от неизвестной функции и(х)и не содержит производных более высокого порядка. Напр., линейное уравнение 2 го порядка имеет вид где точка х (х 1, х 2, ..., х п)принадлежит нек рой… … Математическая энциклопедия
Уравнение, содержащее неизвестную функцию под знаками дифференциальных и интегральных операций. И. д. у. включают и интегральные и дифференциальные уравнения. Линейные И. д. у. Пусть f(x) заданная функция, дифференциальные выражения с достаточно… … Математическая энциклопедия
- (др. греч. εἰκών) это нелинейное дифференциальное уравнение в частных производных, встречающееся в задачах распространения волн, когда волновое уравнение аппроксимируется с помощью теории ВКБ. Оно является следствием уравнений Максвелла, и… … Википедия
Уравнение вида где есть мультииндекс с целыми неотрицательными где. Аналогично определяется Н. у … Математическая энциклопедия
Нелинейное обыкновенное дифференциальное уравнение 2 го порядка или, в самосопряженной форме, где константа. Точка х=0является для Э. у. особой. Заменой переменной уравнение (1) приводится к виду а заменой к виду После замены переменных и… … Математическая энциклопедия
Уравнение (линейное или нелинейное), в к ром неизвестным является элемент какого либо банахова пространства, конкретного (функционального) или абстрактного, т. е. уравнение вида где Р(х) нек рый, вообще говоря, нелинейный оператор, переводящий… … Математическая энциклопедия
Уравнение неравновесной статистпч. физики, используемое в теории газов, аэродинамике, физике плазмы, теории прохождения частиц через вещество, теории переноса излучения. Решение К. у. определяет функцию распределения дпнамич. состояний одной… … Математическая энциклопедия
Нелинейное обыкновенное дифференциальное уравнение 2 го порядка (*) где функция F(и)удовлетворяет предположению: Р. у. описывает типичную нелинейную систему с одной степенью свободы, в к рой возможны автоколебания. Названо по имени Рэлея… … Математическая энциклопедия
Нелинейное обыкновенное дифференциальное уравнение 2 го порядка Является важным частным случаем Лъенара уравнения. В. д. П. у. описывает свободные автоколебания одной из простейших нелинейных колебательных систем (осциллятора Ван дер Поля). В… … Математическая энциклопедия
Дифференциа́льное уравне́ние - уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами). Порядок входящих в уравнение производных может быть различен (формально он ничем не ограничен). Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или все, кроме хотя бы одной производной, отсутствовать вовсе. Не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например, не является дифференциальным уравнением. [
Дифференциальное уравнение порядка выше первого можно преобразовать в систему уравнений первого порядка, в которой число уравнений равно порядку исходного уравнения.
Современные быстродействующие ЭВМ эффективно дают численное решение обыкновенных дифференциальных уравнений, не требуя получения его решения в аналитическом виде. Это позволило некоторым исследователям утверждать, что решение задачи получено, если её удалось свести к решению обыкновенного дифференциального уравнения.
Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения (ОДУ) - это уравнения, зависящие от одной независимой переменной; они имеют вид
Или ![]()
где - неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от независимой переменной штрих означает дифференцирование по Число называется порядком дифференциального уравнения. Наиболее практически важными являются дифференциальные уравнения первого и второго порядка.
Порядок дифференциального уравнения
Порядком дифференциального уравнения называют наивысший порядок производной, входящей в данное уравнение.
Простейшие дифференциальные уравнения первого порядка
Простейшие дифференциальные уравнения первого порядка - класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию. К нему относятся уравнения в полных дифференциалах, уравнения с разделяющимися переменными, однородные уравнения первого порядка и линейные уравнения первого порядка. Все эти уравнения можно проинтегрировать в конечном виде.
Отправной точкой изложения будет служить дифференциальное уравнение первого порядка, записанное в т. н. симметричной форме:
где функции и определены и непрерывны в некоторой области .
Дифференциальные уравнения в частных производных
Дифференциальные уравнения в частных производных (УРЧП) - это уравнения, содержащие неизвестные функции от нескольких переменных и их частные производные. Общий вид таких уравнений можно представить в виде:
где - независимые переменные, а - функция этих переменных. Порядок уравнений в частных производных может определяется так же, как для обыкновенных дифференциальных уравнений. Ещё одной важной классификацией уравнений в частных производных является их разделение на уравнения эллиптического, параболического и гиперболического типа, в особенности для уравнений второго порядка.
Линейные и нелинейные дифференциальные уравнения
Как обыкновенные дифференциальные уравнения, так и уравнения в частных производных можно разделить на линейные и нелинейные . Дифференциальное уравнение является линейным, если неизвестная функция и её производные входят в уравнение только в первой степени (и не перемножаются друг с другом). Для таких уравнений решения образуют аффинное подпространство пространства функций. Теория линейных ДУ развита значительно глубже, чем теория нелинейных уравнений. Общий вид линейного дифференциального уравнения n -го порядка:
где p i (x ) - известные функции независимой переменной, называемые коэффициентами уравнения. Функция r (x ) в правой части называется свободным членом (единственное слагаемое, не зависящее от неизвестной функции) Важным частным классом линейных уравнений являются линейные дифференциальные уравнения с постоянными коэффициентами .
Подклассом линейных уравнений являются однородные дифференциальные уравнения - уравнения, которые не содержат свободного члена: r (x ) = 0. Для однородных дифференциальных уравнений выполняется принцип суперпозиции: линейная комбинация частных решений такого уравнения также будет его решением. Все остальные линейные дифференциальные уравнения называются неоднородными дифференциальными уравнениями.
Нелинейные
дифференциальные уравнения в общем
случае не имеют разработанных методов
решения, кроме некоторых частных классов.
В некоторых случаях (с применением тех
или иных приближений) они могут быть
сведены к линейным. Например, линейное
уравнение гармонического
осциллятора ![]() может
рассматриваться как приближение
нелинейного уравнения математического
маятника
может
рассматриваться как приближение
нелинейного уравнения математического
маятника ![]() для
случая малых амплитуд, когда y
≈
sin y
.
для
случая малых амплитуд, когда y
≈
sin y
.
Мы переходим к рассмотрению уравнений с частными производными первого порядка в общем случае. Как и для рассмотренных выше линейных уравнений, мы сначала будем предполагать, что имеются лишь две независимые переменные. Уравнение с частными производными первого порядка для функции от двух независимых переменных имеет вид
Выясним прежде всего геометрический смысл написанного уравнения. В любой фиксированной точке уравнение (59) представляет собою соотношение между т. е. соотношение между направляющими косинусами нормали к поверхности. Удовлетворяющие этому соотношению нормали образуют некоторую коническую поверхность с вершиной Плоскости, проходящие через точку и перпендикулярные к образующим этого конуса, представляют собою возможные положения
касательной плоскости в фиксированной точке к искомым интегральным поверхностям. Это семейство плоскостей, так же как и семейство образующих конуса нормалей, будет зависеть от одного параметра. Огибающая этого семейства плоскостей будет представлять собою новый конус, который мы назовем конусом Т. Уравнение (59) эквивалентно, таким образом, заданию в каждой точке пространства конуса T, а искомая интегральная поверхность уравнения (59) должна обладать тем свойством, что в каждой ее точке касательная плоскость должна касаться конуса T, соответствующего этой точке.
Составим уравнения образующих конуса Т в заданной точке Пусть и q - функции некоторого параметра а, удовлетворяющие уравнению (59) в фиксированной точке Конус Т является огибающей семейства плоскостей:
Дифференцируя по параметру а, получаем добавочное уравнение
Дифференцируя по а соотношение (59), мы получим
![]()
![]()
В дальнейшем мы будем считать, что при рассматриваемых значениях переменных одновременно в нуль не обращаются, т. е. Исключением будет лишь случай особых решений уравнения (59). Считая, что - и не могут быть оба одновременно равны нулю, мы из однородных уравнений (61) и (62) получаем
![]()
и, наконец, уравнение (60) дает нам окончательно уравнение образующих конуса:
![]()
Чтобы получить различные образующие конуса Т, мы должны в знаменатели подставлять различные значения к q, удовлетворяющие соотношению (59) в фиксированной точке .
В случае линейного уравнения (2) мы имели в каждой точке одно определенное направление, и касательная плоскость к искомым интегральным поверхностям должна была содержать это направление В данном случае мы имеем в каждой точке вместо одного определенного направления конус , и касательная плоскость к искомым интегральным поверхностям должна касаться этого конуса Мы не можем, таким образом, для нелинейного уравнения (59) строить непосредственно характеристические кривые так, как это мы делали для линейного уравнения (2), имея определенное поле направлений. В данном случае вместо поля направлений мы имеем поле конусов Т. Но мы покажем сейчас, что, имея интегральную поверхность уравнения (59), мы можем покрыть ее линиями, которые вполне аналогичны характеристическим линиям линейного уравнения (2). Действительно, в каждой точке интегральной поверхности касательная плоскость должна касаться конуса T, соответствующего этой точке, и, тем самым, должна содержать одну из образующих этого конуса, вдоль которой она и касается конуса Эти образующие конусов Т в различных точках поверхности создают на интегральной поверхности некоторое поле направлений и, тем самым, интегрируя соответствующее этому полю направлений дифференциальное уравнение первого порядка, мы покрываем нашу поверхность семейством кривых T, зависящим от одного параметра. Направляющие косинусы упомянутого поля направлений должны быть пропорциональны знаменателям уравнения (64), где и q определяются непосредственно из уравнения рассматриваемой интегральной поверхности . Таким образом, вдоль упомянутых линий, покрывающих заданную интегральную поверхность, должно выполняться соотношение
![]()
Чтобы найти упомянутые линии на заданной интегральной поверхности, достаточно проинтегрировать уравнение первого порядка
![]()
причем знаменатели написанных дробей содержат только переменные х и у, поскольку функция а и ее частные производные и q на заданной поверхности являются известными функциями х и у. Интегрируя уравнение (67) и пользуясь уравнением поверхности мы и получим упомянутые выше линии
Правые части уравнений (66) имеют определенный смысл только при определенном выборе интегральной поверхности и . Знание интегральной поверхности дает нам и q как функции от . Мы дополним сейчас систему уравнений (66) еще двумя уравнениями, содержащими дифференциалы так, чтобы получилась система дифференциальных уравнений, не зависящая от выбора интегральной поверхности уравнения (59). Обозначим через и t вторые производные функции и:
а через обозначим производные от левой части уравнения (59) по :
Дифференцируя левую часть уравнения (55) по х и у полным образом, мы получим
С другой стороны, мы имеем, очевидно,

Из написанных уравнений непосредственно вытекает, что
и, следовательно, мы можем добавить к уравнениям (66) еще два последних уравнения, и, таким образом, получим следующую систему пяти дифференциальных уравнений с пятью функциями вспомогательного параметра
Часто одно лишь упоминание дифференциальных уравнений вызывает у студентов неприятное чувство. Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение дифуров становиться просто пыткой. Ничего не понятно, что делать, как решать, с чего начать?
Однако мы постараемся вам показать, что дифуры – это не так сложно, как кажется.
Основные понятия теории дифференциальных уравнений
Со школы нам известны простейшие уравнения, в которых нужно найти неизвестную x. По сути дифференциальные уравнения лишь чуточку отличаются от них – вместо переменной х в них нужно найти функцию y(х) , которая обратит уравнение в тождество.
Дифференциальные уравнения имеют огромное прикладное значение. Это не абстрактная математика, которая не имеет отношения к окружающему нас миру. С помощью дифференциальных уравнений описываются многие реальные природные процессы. Например, колебания струны, движение гармонического осциллятора, посредством дифференциальных уравнений в задачах механики находят скорость и ускорение тела. Также ДУ находят широкое применение в биологии, химии, экономике и многих других науках.
Дифференциальное уравнение (ДУ ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.
Существует множество видов дифференциальных уравнений: обыкновенные дифференциальные уравнения, линейные и нелинейные, однородные и неоднородные, дифференциальные уравнения первого и высших порядков, дифуры в частных производных и так далее.
Решением дифференциального уравнения является функция, которая обращает его в тождество. Существуют общие и частные решения ДУ.
Общим решением ДУ является общее множество решений, обращающих уравнение в тождество. Частным решением дифференциального уравнения называется решение, удовлетворяющее дополнительным условиям, заданным изначально.
Порядок дифференциального уравнения определяется наивысшим порядком производных, входящих в него.

Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения – это уравнения, содержащие одну независимую переменную.
Рассмотрим простейшее обыкновенное дифференциальное уравнение первого порядка. Оно имеет вид:

Решить такое уравнение можно, просто проинтегрировав его правую часть.
Примеры таких уравнений:

Уравнения с разделяющимися переменными
В общем виде этот тип уравнений выглядит так:

Приведем пример:

Решая такое уравнение, нужно разделить переменные, приведя его к виду:

После этого останется проинтегрировать обе части и получить решение.

Линейные дифференциальные уравнения первого порядка
Такие уравнения имеют вид:

Здесь p(x) и q(x) – некоторые функции независимой переменной, а y=y(x) – искомая функция. Приведем пример такого уравнения:

Решая такое уравнение, чаще всего используют метод вариации произвольной постоянной либо представляют искомую функцию в виде произведения двух других функций y(x)=u(x)v(x).
Для решения таких уравнений необходима определенная подготовка и взять их “с наскока” будет довольно сложно.
Пример решения ДУ с разделяющимися переменными
Вот мы и рассмотрели простейшие типы ДУ. Теперь разберем решение одного из них. Пусть это будет уравнение с разделяющимися переменными.

Сначала перепишем производную в более привычном виде:

Затем разделим переменные, то есть в одной части уравнения соберем все "игреки", а в другой – "иксы":

Теперь осталось проинтегрировать обе части:

Интегрируем и получаем общее решение данного уравнения:

Конечно, решение дифференциальных уравнений – своего рода искусство. Нужно уметь понимать, к какому типу относится уравнение, а также научиться видеть, какие преобразования нужно с ним совершить, чтобы привести к тому или иному виду, не говоря уже просто об умении дифференцировать и интегрировать. И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию , обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему "Как решать дифференциальные уравнения":
Содержание статьи
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Многие физические законы, которым подчиняются те или иные явления, записываются в виде математического уравнения, выражающего определенную зависимость между какими-то величинами. Часто речь идет о соотношении между величинами, изменяющимися с течением времени, например экономичность двигателя, измеряемая расстоянием, которое автомашина может проехать на одном литре горючего, зависит от скорости движения автомашины. Соответствующее уравнение содержит одну или несколько функций и их производных и называется дифференциальным уравнением. (Темп изменения расстояния со временем определяется скоростью; следовательно, скорость – производная от расстояния; аналогично, ускорение – производная от скорости, так как ускорение задает темп изменения скорости со временем.) Большое значение, которое имеют дифференциальные уравнения для математики и особенно для ее приложений, объясняются тем, что к решению таких уравнений сводится исследование многих физических и технических задач. Дифференциальные уравнения играют существенную роль и в других науках, таких, как биология, экономика и электротехника; в действительности, они возникают везде, где есть необходимость количественного (числового) описания явлений (коль скоро окружающий мир изменяется во времени, а условия изменяются от одного места к другому).
Примеры.
Следующие примеры позволяют лучше понять, как различные задачи формулируются на языке дифференциальных уравнений.
1) Закон распада некоторых радиоактивных веществ состоит в том, что скорость распада пропорциональна наличному количеству этого вещества. Если x – количество вещества в некоторый момент времени t , то этот закон можно записать так:
где dx /dt – скорость распада, а k – некоторая положительная постоянная, характеризующая данное вещество. (Знак «минус» в правой части указывает на то, что x убывает со временем; знак «плюс», подразумеваемый всегда, когда знак явно не указан, означал бы, что x возрастает со временем.)
2) Емкость первоначально содержит 10 кг соли, растворенной в 100 м 3 воды. Если чистая вода вливается в емкость со скоростью 1 м 3 в минуту и равномерно перемешивается с раствором, а образовавшийся раствор вытекает из емкости с такой же скоростью, то сколько соли окажется в емкости в любой последующий момент времени? Если x – количество соли (в кг) в емкости в момент времени t , то в любой момент времени t в 1 м 3 раствора в емкости содержится x /100 кг соли; поэтому количество соли убывает со скоростью x /100 кг/мин, или
3) Пусть на тело массы m , подвешенное к концу пружины, действует возвращающая сила, пропорциональная величине растяжения пружины. Пусть x – величина отклонения тела от положения равновесия. Тогда по второму закону Ньютона, который утверждает, что ускорение (вторая производная от x по времени, обозначаемая d 2 x /dt 2) пропорционально силе:
Правая часть стоит со знаком минус потому, что возвращающая сила уменьшает растяжение пружины.
4) Закон охлаждения тел утверждает, что количество тепла в теле убывает пропорционально разности температур тела и окружающей среды. Если чашка кофе, разогретого до температуры 90° С находится в помещении, температура в котором равна 20° С, то
где T – температура кофе в момент времени t .
5) Министр иностранных дел государства Блефуску утверждает, что принятая Лиллипутией программа вооружений вынуждает его страну увеличить военные расходы на сколько это только возможно. С аналогичными заявлениями выступает и министр иностранных дел Лиллипутии. Возникающую в результате ситуацию (в простейшей интерпретации) можно точно описать двумя дифференциальными уравнениями. Пусть x и y – расходы на вооружение Лиллипутии и Блефуску. Предполагая, что Лиллипутия увеличивает свои расходы на вооружение со скоростью, пропорциональной скорости увеличения расходов на вооружение Блефуску, и наоборот, получаем:
где члены -ax и -by описывают военные расходы каждой из стран, k и l – положительные постоянные. (Эту задачу впервые таким образом сформулировал в 1939 Л.Ричардсон.)
После того, как задача записана на языке дифференциальных уравнений, следует попытаться их решить, т.е. найти величины, скорости изменения которых входят в уравнения. Иногда решения находятся в виде явных формул, но чаще их удается представить лишь в приближенном виде или же получить о них качественную информацию. Часто бывает трудно установить, существует ли решение вообще, не говоря уже о том, чтобы найти его. Важный раздел теории дифференциальных уравнений составляют так называемые «теоремы существования», в которых доказывается наличие решения у того или иного типа дифференциальных уравнений.
Первоначальная математическая формулировка физической задачи обычно содержит упрощающие предположения; критерием их разумности может служить степень согласованности математического решения с имеющимися наблюдениями.
Решения дифференциальных уравнений.
Дифференциальному уравнению, например dy /dx = x /y , удовлетворяет не число, а функция, в данном конкретном случае такая, что ее график в любой точке, например в точке с координатами (2,3), имеет касательную с угловым коэффициентом, равным отношению координат (в нашем примере 2/3). В этом нетрудно убедиться, если построить большое число точек и от каждой отложить короткий отрезок с соответствующим наклоном. Решением будет функция, график которой касается каждой своей точкой соответствующего отрезка. Если точек и отрезков достаточно много, то мы можем приближенно наметить ход кривых-решений (три такие кривые показаны на рис. 1). Существует ровно одна кривая-решение, проходящая через каждую точку с y № 0. Каждое отдельное решение называется частным решением дифференциального уравнения; если удается найти формулу, содержащую все частные решения (за исключением, быть может, нескольких особых), то говорят, что получено общее решение. Частное решение представляет собой одну функцию, в то время как общее – целое их семейство. Решить дифференциальное уравнение – это значит найти либо его частное, либо общее решение. В рассматриваемом нами примере общее решение имеет вид y 2 – x 2 = c , где c – любое число; частное решение, проходящее через точку (1,1), имеет вид y = x и получается при c = 0; частное решение, проходящее через точку (2,1), имеет вид y 2 – x 2 = 3. Условие, требующее, чтобы кривая-решение проходила, например, через точку (2,1), называется начальным условием (так как задает начальную точку на кривой-решении).
Можно показать, что в примере (1) общее решение имеет вид x = ce –kt , где c – постоянная, которую можно определить, например, указав количество вещества при t = 0. Уравнение из примера (2) – частный случай уравнения из примера (1), соответствующий k = 1/100. Начальное условие x = 10 при t = 0 дает частное решение x = 10e –t /100 . Уравнение из примера (4) имеет общее решение T = 70 + ce –kt и частное решение 70 + 130 –kt ; чтобы определить значение k , необходимы дополнительные данные.
Дифференциальное уравнение dy /dx = x /y называется уравнением первого порядка, так как содержит первую производную (порядком дифференциального уравнения принято считать порядок входящей в него самой старшей производной). У большинства (хотя и не у всех) возникающих на практике дифференциальных уравнений первого рода через каждую точку проходит только одна кривая-решение.
Существует несколько важных типов дифференциальных уравнений первого порядка, допускающих решения в виде формул, содержащих только элементарные функции – степени, экспоненты, логарифмы, синусы и косинусы и т.д. К числу таких уравнений относятся следующие.
Уравнения с разделяющимися переменными.
Уравнения вида dy /dx = f (x )/g (y ) можно решить, записав его в дифференциалах g (y )dy = f (x )dx и проинтегрировав обе части. В худшем случае решение представимо в виде интегралов от известных функций. Например, в случае уравнения dy /dx = x /y имеем f (x ) = x , g (y ) = y . Записав его в виде ydy = xdx и проинтегрировав, получим y 2 = x 2 + c . К уравнениям с разделяющимися переменными относятся уравнения из примеров (1), (2), (4) (их можно решить описанным выше способом).
Уравнения в полных дифференциалах.
Если дифференциальное уравнение имеет вид dy /dx = M (x ,y )/N (x ,y ), где M и N – две заданные функции, то его можно представить как M (x ,y )dx – N (x ,y )dy = 0. Если левая часть является дифференциалом некоторой функции F (x ,y ), то дифференциальное уравнение можно записать в виде dF (x ,y ) = 0, что эквивалентно уравнению F (x ,y ) = const. Таким образом, кривые-решения уравнения – это «линии постоянных уровней» функции, или геометрические места точек, удовлетворяющих уравнениям F (x ,y ) = c . Уравнение ydy = xdx (рис. 1) – с разделяющимися переменными, и оно же – в полных дифференциалах: чтобы убедиться в последнем, запишем его в виде ydy – xdx = 0, т.е. d (y 2 – x 2) = 0. Функция F (x ,y ) в этом случае равна (1/2)(y 2 – x 2); некоторые из ее линий постоянного уровня представлены на рис. 1.
Линейные уравнения.
Линейные уравнения – это уравнения «первой степени» – неизвестная функция и ее производные входят в такие уравнения только в первой степени. Таким образом, линейное дифференциальное уравнение первого порядка имеет вид dy /dx + p (x ) = q (x ), где p (x ) и q (x ) – функции, зависящие только от x . Его решение всегда можно записать с помощью интегралов от известных функций. Многие другие типы дифференциальных уравнений первого порядка решаются с помощью специальных приемов.
Уравнения старших порядков.
Многие дифференциальные уравнения, с которыми сталкиваются физики, это уравнения второго порядка (т.е. уравнения, содержащие вторые производные) Таково, например, уравнение простого гармонического движения из примера (3), md 2 x /dt 2 = –kx . Вообще говоря, можно ожидать, что уравнение второго порядка имеет частные решения, удовлетворяющие двум условиям; например, можно потребовать, чтобы кривая-решение проходила через данную точку в данном направлении. В случаях, когда дифференциальное уравнение содержит некоторый параметр (число, величина которого зависит от обстоятельств), решения требуемого типа существуют только при определенных значениях этого параметра. Например, рассмотрим уравнение md 2 x /dt 2 = –kx и потребуем, чтобы y (0) = y (1) = 0. Функция y є 0 заведомо является решением, но если – целое кратное числа p , т.е. k = m 2 n 2 p 2, где n – целое число, а в действительности только в этом случае, существуют другие решения, а именно: y = sin npx . Значения параметра, при которых уравнение имеет особые решения, называются характеристическими или собственными значениями; они играют важную роль во многих задачах.
Уравнение простого гармонического движения служит примером важного класса уравнений, а именно: линейных дифференциальных уравнений с постоянными коэффициентами. Более общий пример (также второго порядка) – уравнение
где a и b – заданные постоянные, f (x ) – заданная функция. Такие уравнения можно решать различными способами, например, с помощью интегрального преобразования Лапласа. То же можно сказать и о линейных уравнениях более высоких порядков с постоянными коэффициентами. Не малую роль играют также и линейные уравнения с переменными коэффициентами.
Нелинейные дифференциальные уравнения.
Уравнения, содержащие неизвестные функции и их производные в степени выше первой или каким-либо более сложным образом, называются нелинейными. В последние годы они привлекают все большее внимание. Дело в том, что физические уравнения обычно линейны лишь в первом приближении; дальнейшее и более точное исследование, как правило, требует использования нелинейных уравнений. Кроме того, многие задачи нелинейны по своей сути. Так как решения нелинейных уравнений зачастую очень сложны и их трудно представить простыми формулами, значительная часть современной теории посвящена качественному анализу их поведения, т.е. разработке методов, позволяющих, не решая уравнения, сказать нечто существенное о характере решений в целом: например, что все они ограниченны, или имеют периодический характер, или определенным образом зависят от коэффициентов.
Приближенные решения дифференциальных уравнений могут быть найдены в численном виде, но для этого требуется много времени. С появлением быстродействующих компьютеров это время сильно сократилось, что открыло новые возможности численного решения многих, ранее не поддававшихся такому решению, задач.
Теоремы существования.
Теоремой существования называется теорема, утверждающая, что при определенных условиях данное дифференциальное уравнение имеет решение. Встречаются дифференциальные уравнения, не имеющие решений или имеющие их больше, чем ожидается. Назначение теоремы существования – убедить нас в том, что у данного уравнения действительно есть решение, а чаще всего заверить, что оно имеет ровно одно решение требуемого типа. Например, уже встречавшееся нам уравнение dy /dx = –2y имеет ровно одно решение, проходящее через каждую точку плоскости (x ,y ), а так как одно такое решение мы уже нашли, то тем самым полностью решили это уравнение. С другой стороны, уравнение (dy /dx ) 2 = 1 – y 2 имеет много решений. Среди них прямые y = 1, y = –1 и кривые y = sin(x + c ). Решение может состоять из нескольких отрезков этих прямых и кривых, переходящих друг в друга в точках касания (рис. 2).
Дифференциальные уравнения в частных производных.
Обыкновенное дифференциальное уравнение – это некоторое утверждение о производной неизвестной функции одной переменной. Дифференциальное уравнение в частных производных содержит функцию двух или более переменных и производные от этой функции по крайней мере по двум различных переменным.
В физике примерами таких уравнений являются уравнение Лапласа
X , y ) внутри круга, если значения u заданы в каждой точке ограничивающей окружности. Поскольку проблемы с более чем одной переменной в физике являются скорее правилом, чем исключением, легко представить, сколь обширен предмет теории дифференциальных уравнений в частных производных.